


Next: Radici di un polinomio
Up: Gli errori
Previous: Gli errori
Vogliamo risolvere su [0,10] il problema
la cui soluzione esatta è
y(x)=e-x. Osserviamo per prima cosa che
se poniamo la condizione iniziale
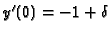 (con
(con 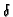 piccolo), la soluzione esatta del problema
diventerebbe
piccolo), la soluzione esatta del problema
diventerebbe
che è profondamente diversa dalla precedente (non tende neppure a 0 quando
x va ad infinito). Questo mostra che il problema è molto sensibile ai dati
iniziali, dunque è malcondizionato. Non possiamo aspettarci grandi risultati
dall'algoritmo risolutivo che adesso viene esposto.
Per risolvere l'equazione numericamente, l'idea è di discretizzare
l'intervallo: scelto un opportuno passo h, si
utilizzano solo i valori che y assume nei punti
x+ih (per
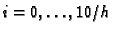 .
Poniamo dunque
.
Poniamo dunque
yi = y(x+ih).
Si pone il problema di approssimare l'operatore ``derivata seconda''.
A tale scopo, utilizzando la formula di Taylor, si può ricavare che
da cui otteniamo
L'equazione iniziale si scrive allora
yi+1 = (2+h2) yi -yi-1
e l'applicazione ripetuta di questa formula a partire da due valori
iniziali
y0=1, y-1=eh dovrebbe permetterci di ricavare
i valori successivi di y(x+ih).
L'implementazione (esemplificata in diffeq.c) mostra
invece che questo sistema dà, dopo poche iterazioni, risultati addirittura
negativi. In questo caso, come detto, è il problema ad essere fortemente
malcondizionato. Esso va dunque trattato con metodi molto particolari.



Next: Radici di un polinomio
Up: Gli errori
Previous: Gli errori
Daniele Finocchiaro
1998-11-13
![]() .
Poniamo dunque
.
Poniamo dunque